Automating the Measurement of Frequency Response

Recently I wanted to measure and plot the frequency response of one of my amps at various settings of the tone controls. It seemed like it should be an easy task. I'd simply connect a signal generator and an oscilloscope to the amp, and then write down the output signal levels at a bunch of different frequencies. Then I'd enter the numbers into a spreadsheet or some other plotting program, and display the results. So, I hooked everything up and got started.

It took only a few minutes for me to realize what a boring, tedious chore I had taken on. To generate a reasonably smooth plot, I'd need to take measurements at many different frequencies. The output level of my signal generator wasn't precisely the same over the entire audio frequency range, so I had to check it and adjust it at each step of the way. And it's not at all easy to read a signal level from an oscilloscope with much precision at all. I considered using a digital multimeter to measure the signal levels, but most DMMs are accurate only up to about 1 kHz on their AC ranges.

Surely there must be a way to take some of the tedium out of the process. What if I could automate it? I had a spare Raspberry Pi lying around. (The Raspberry Pi is a tiny $35 computer that runs Linux and has a bunch of I/O pins for controlling external hardware.) All I'd need to do would be to add a handful of external components and write a little software. No problem! So I started working on it.

In this way, I transformed a painfully boring 2-hour task into a fun and interesting month-long project—a clear win!

The block diagram nearby shows the design I ended up with. The rest of the article goes into some detail about the component parts.

Generating the Test Signal

The first step was to generate sine waves at specified frequencies under software control. Since the Raspberry Pi has an audio output, I decided to see if I could generate sine waves with it. After some research, I found the pyalsaaudio package for the Python programming language, and managed to use it to generate sine waves on the audio output. This took quite a bit of effort. The software has to calculate samples of the sine wave (48000 samples per second) in real time and send them on to the audio driver. It took quite a bit of code to do that.

Unfortunately, the audio output of the Raspberry Pi is not what anyone would call high-fidelity. The computer generates the signal using pulse-width modulation. It's quite noisy, and there's a lot of high-frequency hash superimposed on the signal. I was able to clean it up significantly by adding a second-order low-pass filter, but it was hard to eliminate the hash without also attenuating the desired signal at higher audio frequencies. (I wanted to be able to measure frequency response over the two-decade range of 100 Hz to 10 kHz.) Nevertheless, I was able to generate some reasonable plots by compensating for the filter roll-off in software.

Meanwhile, I kept looking for a better solution. I found it in a tiny signal generator module based on the Analog Devices AD9833 chip. This amazing and inexpensive device generates beautiful sine, square, or triangle waves at frequencies ranging from 0.1 Hz. to around 10 MHz, controllable to a resolution of about 0.1 Hz. It can interface directly to the Raspberry Pi's SPI bus without any "glue" logic. Controlling it in software is trivial; you simply tell it what frequency to produce, and it does the rest. The output waveforms are nice and clean, and the signal level is constant over the entire frequency range. Needless to say, I abandoned the Raspberry Pi's audio output and used the AD9833 device instead.

Measuring the Output Response

The other half of the task was to measure the signal level at the output of the amp being tested. Doing so requires converting the AC signal at the output of the amp into a proportional DC voltage that can be fed into an analog-to-digital converter (ADC). This turned out to be a bit of a challenge. In power supplies, we simply rectify the AC to DC, but with low-level audio signals that method is inaccurate, due to the forward voltage drop of the diodes.

There exist simple op amp based circuits to eliminate the diode error (google "peak detectors"). But these circuits place heavy demands on their op amps, and their frequency response is very poor. That is why most DMMs cannot measure AC voltages above a kilohertz or so. Nevertheless, I used such a peak detector circuit at first, and was able to get acceptable results by compensating for the poor frequency response in software.

Later, I found a much better solution. The basic idea is to rectify the signal, keeping only the positive half-cycles. If I could do that accurately, then I could pass the positive half-cycles through a low-pass filter to find their average value, which would be directly proportional to the signal level. The tricky part is the rectification, which must be precise—without any inaccuracies from diode drops. Eventually, in an op amp application note, I found a very clever solution.

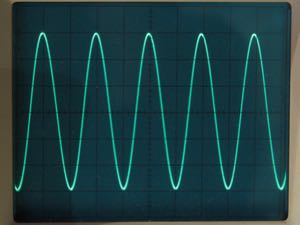
The trick is to use a single-supply, rail-to-rail op amp in a simple voltage-follower configuration. "Single-supply" means the op amp runs from a single voltage source, e.g., +5V, as opposed to the dual positive and negative supplies that were traditionally used for op amps. "Rail-to-rail" means two things. First, it means the op amp can still amplify properly even when its inputs swing all the way to ground or to the positive supply voltage, and even beyond those points by about 300 mV. Second, it means the op amp can drive its output almost all the way to ground or to the positive supply voltage—within a few millivolts, typically.

When such an op amp is wired as a voltage-follower with its input biased at ground potential, it functions as a nearly perfect rectifier. Positive swings of the input signal are amplified normally, at unity gain. Negative swings of the input are clipped, because the op amp cannot drive its output below ground potential. One important caveat is that you must drive the input of the op amp through a resistor. Since the input swings far below ground potential, the resistor is necessary to limit the current into the op amp in order to keep from destroying it. Op amp datasheets specify the maximum current allowed, and a suitable resistor can be calculated from that and from the expected maximum signal amplitude. In my case, a 10k resistor was a reasonable choice.

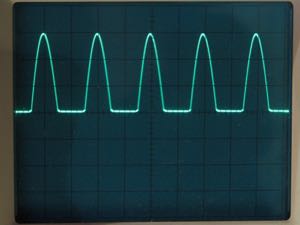
This simple circuit has excellent frequency response. I used an MCP6022 dual op amp chip, with a gain-bandwidth product of 10 Mhz, and found that it performed very well at frequencies up to several hundred kilohertz. The scope photos nearby show the input and output of the circuit. When the two waveforms are superimposed on the scope screen, their top halves line up perfectly even at high frequencies.

After rectification, the signal is filtered by a simple RC low-pass filter to remove the AC component, leaving only the DC average voltage. The mean value of a half-wave rectified sine wave is A/π, where A is the peak amplitude of the signal. Since the precision rectifier circuit can put out signals of 5V peak (the supply voltage) before clipping, the maximum filtered voltage will be 5/π, or 1.592V. The ADC that I used (MCP3004 with an MCP1541 voltage reference) has a full-scale input voltage of 4.092V. I used the second op amp of the MCP6022 to amplify the filtered DC by a factor of 3. This ensures two things. First, the full range of the ADC is utilized, improving accuracy. Second, the ADC reaches full scale before the precision rectifier starts to clip the positive peaks of the signal.

Putting it All Together

The photo at right shows the prototype circuit. As you can see, there's not much to it. (By the way, please don't email me asking for detailed schematics or software. This article is all I've got for you.) The red header on the left side connects to the Raspberry Pi's I/O pins. Next to it is a ULN2803A darlington array for buffering the signals and converting between the Raspberry Pi's 3.3V logic and the 5V logic used in the rest of the circuit. Next comes the MCP3004 ADC, then the MCP6022 dual op amp, and finally the AD9833 signal generator board.

One convenient thing about this circuit is that it needs only a single 5V power supply. Because of that, it can be powered directly from the Raspberry Pi.

Performance

I'm very pleased with the performance of the device. At present I have the software set to measure 401 logarithmically-spaced frequencies from 100 Hz to 10 kHz. The software waits 1 second after each frequency change, in order to allow the filtered DC to settle fully. (The low-pass filter has a long time constant.) So, a full sweep takes less than 7 minutes, with no operator intervention required. A more sophisticated low-pass filter could make it faster, but it's hardly worth the effort or the extra hardware.

I checked the frequency response of the device itself by connecting its output directly to its input, and then running a sweep. The response was flat within just a few tenths of a dB—quite acceptable.

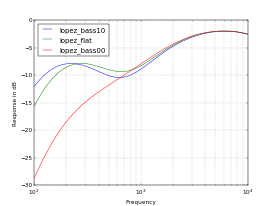
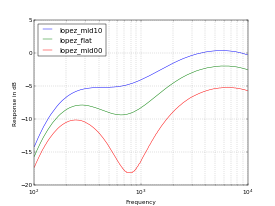
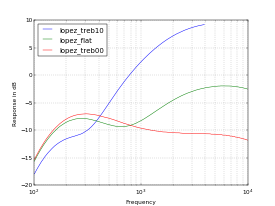
Shown below (click to enlarge) are four plots made by the device. The first three plots are from an amp I built that has a Fender-style tone stack. They show the actions of the bass, midrange, and treble controls, respectively, with the other tone controls set to 5.

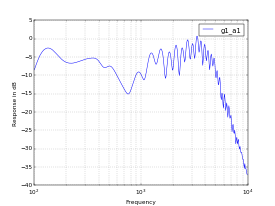
I was quite surprised when I saw the fourth plot. It is from a Zoom G1on multi-effects pedal. Some time ago, I created a patch on the G1on that I use for practing my pedal steel guitar with headphones. The patch is made up of a 1965 Fender Twin Reverb amp model feeding into a model of a 1963 Fender reverb unit. It sounds really good through headphones for my pedal steel, so I was interested to see a plot of its frequency response. I disabled the reverb to make the plot, since the time-varying nature of reverb wreaks havoc with the measurement process.

The surprising thing about this plot is the squiggly shape of the curve. It is completely repeatable; i.e., it truly represents the frequency response of the patch. I believe the squiggles are a by-product of the digital signal processing that is used in the G1on. I'm reasonbly certain they were not intentional, and I don't hear them when I play through the device. Perhaps that is because the squiggles are fairly minor up to about 1500 Hz, well above the normal range of a pedal steel. Although they must affect the harmonics of the notes, they don't have much influence on the fundamental frequencies.

UPDATE: User Kursad K of the AX84 Forum explained the true reason for the squiggles in the response curve of the G1on. They come from the amp model's speaker cabinet emulation, and according to Kursad they closely resemble the response curves of real speaker cabinets. And sure enough, after I disabled the speaker cabinet emulation, I obtained a very different plot, as shown below:

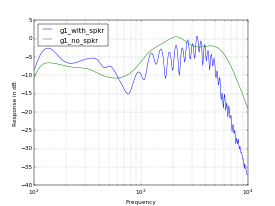
Many thanks to Kursad for straightening me out!